Erdös: The Man Who Loved Only Numbers
Assignments for Class #4
• Read Chapter e, pages 95-130.
• Read "Figures of Thought", by Robert Nemerov.
• On the Maths in Pop Culture page, see the latest entry, about an interesting quilt based on the sieve of Eratosthenes.
• Watch this video to learn more about Ulam spirals, and other ways to enhance your chances of finding new prime numbers.
Watch this video, about Russell's paradox and Gödel's proof:
Watch this video, about a very large number:
Questions to Think About
• The chapter title: what is e, anyway?
• James Grime, in the first video above (about Ulam spirals), expresses some of the diagonal lines as quadratic equations, and then says that we have some formulas and equations that "have more prime numbers than others." What does he mean?
• Try to make up a statement or question that is self-contradictory. Submit your efforts using the form at the bottom of this page.
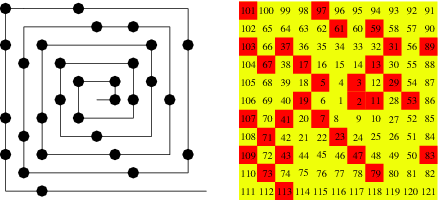
• Use this table of prime numbers to compare the number of primes from 1 to 100 with the number of primes from 1,000 to 1,100 and with the number of primes from 10,000 to 10,100. How many primes are within each of these ranges? What do you discover and conjecture?
• What is the difference - qualitatively - between the two curves shown in this picture? (the picture you see in the upper-right-hand corner of the page)
(If the words qualitative and quantitative are not among your old friends, look them up, and then make up an example of a qualitative difference and a quantitative difference.)
Other Resources
• Here is a Ulam spiral starting with 1 in the middle. For more about the behavior of primes in these constructions, see this page at Wolfram Mathworld:
• Learn more about Goldbach's conjecture and the twin prime conjecture at Wikipedia (both mentioned in the James Grime's video).
• Continuations of James Grime's story of searching for primes.
-- Using Fermat's Little Theorem
-- A Foolproof test for primes:
• Here is a much more detailed presentation about Gödel's proof, from the excellent YouTube channel Veritasium. Steve and I feel that the channel host, Derek Müller, overstates the "problem" this proof poses for all of mathematics, but otherwise, the video is up to Derek's usual high standards.
• Wikipedia: List of Undecidable Problems
Do any real and practical mathematical problems ever run into the kinds of problems that are the focus of Gödel's proof? This Wikipedia entry is an extensive (but not complete) list of problems proven to be undecidable.
One of the listed undecidable problems involves John Conway's Game of Life, specifically: "Conway's Game of Life on whether given an initial pattern and another pattern, can the latter pattern ever appear from the initial one."
Another undecidable problem: The problem of planning optimal air travel from one destination to another, when fares are taken into account. (de Marcken, Carl. "Computational Complexity of Air Travel Planning" (PDF). ITA Software.)
••••••
Looking Ahead to Class #5
• As a preview of next week's class (Class #5, chapter 3, the fifth chapter), think a bit about relative prime numbers. The topic is not in the index of the text, but see pages 38 and 132 (I added these entries to the index of my copy.)
(Remember that 1 is not a prime number. Some people call 0 and 1 pre-primes, meaning that they come before the "real" primes. Some people include 2 in the pre-primes; the term pre-prime is informal, not a common technical term.)
Two integers that have no prime factors in common are called relative primes. The first pair of relative primes are 2 and 3.
- What is the next pair of relative primes after 2 and 3?
- Are any two primes a relative pair?
- Are there two even numbers that make a relative pair?
- What is the first relative pair in which one number is prime and one is composite?
- What is the first pair of composite numbers that are relative primes?